郑州大学计算智能实验室

Computational Intelligence Laboratory

MMO

The papers here are for faster dissemination and academic research convinence purpose only, and the copyright of the final papers belongs to the corresponding publishers !


Research on Multimodal Multi-objective Problems 


Important activities on Multimodal multiobjective optimization (MMO)

Competition and Special Session on Multimodal Multiobjective Optimization was organized along with the CEC 2021. The competition information is available on http://www5.zzu.edu.cn/ecilab/info/1036/1251.htm.


1. Simple introduction to multimodal multiobjective optimization (MMO)

 

For a multiobjective optimization problem, if it meets one of the following conditions, it is a multimodal multiobjective optimization problem:

1) It has at least one local Pareto optimal solution;

2) It has at least two global Pareto optimal solutions corresponding to the same point on the PF.

The local Pareto optimal solution represents the solution which is not dominated by any neighborhood solution. The global Pareto optimal solution is not dominated by any solutions in the feasible space.

Fig. 1 shows a bi-objective minimization problem with two Global PSs. Note that a certain multimodal multiobjective problem may have several Local PSs and Global PSs.

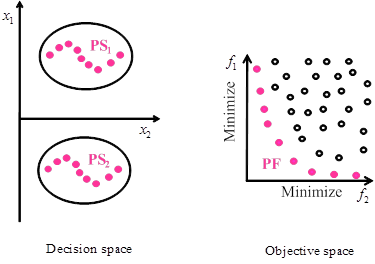
Fig. 1. Illustration of multimodal multiobjective problem.

 

 

2. Multimodal multiobjective optimization (MMO) related reference list

  1. Li W, Zhang T, Wang R, et al. Weighted indicator-based evolutionary algorithm for multimodal multi-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2021.(paper)

  2. Fan Q, Ersoy O K. Zoning Search With Adaptive Resource Allocating Method for Balanced and Imbalanced Multimodal Multi-Objective Optimization[J]. IEEE/CAA Journal of Automatica Sinica, 2021, 8(6): 1163-1176.(paper)

  3. Li Z, Zou J, Yang S, et al. A two-archive algorithm with decomposition and fitness allocation for multi-modal multi-objective optimization[J]. Information Sciences, 2021, 574: 413-430.(paper)

  4. Moshaiov A, Breslav Y, Farhi E. Multi-Modal Multi-Objective Evolutionary Optimization for Problems with Solutions of Variable-Length[C]//2021 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2021: 1193-1200.(paper)

  5. Grimme C, Kerschke P, Aspar P, et al. Peeking beyond peaks: Challenges and research potentials of continuous multimodal multi-objective optimization[J]. Computers & Operations Research, 2021: 105489.(paper)

  6. Q. L. Dang, W. Xu, Y. F. Yuan. A Dynamic Resource Allocation Strategy with Reinforcement Learning for Multimodal Multi-objective Optimization[J]. International Journal of Automation and Computing, 2021, 18: 1-15.(paper)

  7. W. L. Wang, G. Q. Li, Y. L. Wang, F. Wu, W. W. Zhang, L. Li. Clearing-based multimodal multi-objective evolutionary optimization with layer-to-layer strategy[J]. Swarm and Evolutionary Computation, 2021: 100976.(paper)

  8. R. Wang, W. Ma, M. Tan, G. H. Wu, L. Wang, D. W. Gong, J. Xiong. Preference-inspired coevolutionary algorithm with active diversity strategy for multi-objective multi-modal optimization[J]. Information Sciences, 2021(546): 1148-1165.（paper）

  9. C. T. Yue, P. N. Suganthan, J. Liang, B. Y. Qu, K. J. Yu, Y. S. Zhu, Y. Li. Differential evolution using improved crowding distance for multimodal multiobjective optimization[J]. Swarm and Evolutionary Computation, 2021, 62: 100849.（paper）

  10. K. Jha, S. Saha. Incorporation of multimodal multiobjective optimization in designing a filter based feature selection technique[J]. Applied Soft Computing, 2021, 98: 106823.（paper）

  11. M. Pal, S. Bandyopadhyay. Decomposition in decision and objective space for multi-modal multi-objective optimization[J]. Swarm and Evolutionary Computation, 2021, 62: 100842.（paper）

  12. K. Zhang, M. Chen, X. Xu, G. G. Yen. Multi-objective evolution strategy for multimodal multi-objective optimization[J]. Applied Soft Computing, 2021, 101: 107004.（paper）

  13. G. Li, W. Wang, W. Zhang, Z. Wang, H. Tu, W. You. Grid search based multi-population particle swarm optimization algorithm for multimodal multi-objective optimization[J]. Swarm and Evolutionary Computation, 2021: 100843. (paper)

  14. Q. Yang, Z. Wang, J. Luo, Q. He. Balancing performance between the decision space and the objective space in multimodal multiobjective optimization[J]. Memetic Computing, 2021: 1-17. (paper)

  15. M. Javadi, C. R. Atencia, S. Mostaghim. Combining manhattan and crowding distances in decision space for multimodal multi-objective optimization problems[C]//Advances in Evolutionary and Deterministic Methods for Design, Optimization and Control in Engineering and Sciences. Springer, Cham, 2021: 131-145.（paper）

  16. M. Javadi, H. Zille, S. Mostaghim. The effects of crowding distance and mutation in multimodal and multi-objective optimization problems[C]//Advances in Evolutionary and Deterministic Methods for Design, Optimization and Control in Engineering and Sciences. Springer, Cham, 2021: 115-130.（paper）

  17. K. Zhang, C. Shen, J. He, G. G. Yen. Knee based multimodal multi-objective evolutionary algorithm for decision making[J]. Information Sciences, 2021, 544: 39-55.（paper）

  18. C. Liu, W. Shen, L. Zhang, H. Yang, Y. Du, Z. Yuan, H. Zhao. Improved Membrane Algorithm Under the Framework of P Systems to Solve Multimodal Multiobjective Problems[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2021: 2159024.（paper）

  19. N. Luo, W. Lin, P. Huang, J. Chen. An Evolutionary Algorithm with Clustering-Based Assisted Selection Strategy for Multimodal Multiobjective Optimization[J]. Complexity, 2021, 2021.（paper）

  20. Y. Hu, B. Y. Qu, J. Wang, J. Liang, Y. L. Wang, K. J. Yu, Y. X. Li, K. J. Qiao. Short-term load forecasting using multimodal evolutionary algorithm and random vector functional link network based ensemble learning[J]. Applied Energy, 285 (2021): 116415. (paper)

  21. W. Lin, Y. Li, N. Luo. A Novel Decomposition-Based Multimodal Multi-objective Evolutionary Algorithm[C]//International Conference on Intelligent Computing. Springer, Cham, 2020: 571-582. (paper)

  22. C. T. Yue, J. J. Liang, P. N. Suganthan, B. Y. Qu, K. J. Yu, S. Liu. MMOGA for Solving Multimodal Multiobjective Optimization Problems with Local Pareto Sets[C]// 2020 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2020: 1-8. （paper）

  23. G. Li, L. Yan, B. Y. Qu. Multi-Objective Particle Swarm Optimization Based on Gaussian Sampling[J]. IEEE Access, 2020, 8: 209717-209737.（paper）

  24. M. Javadi, C. Ramirez-Atencia. S, Mostaghim. A Novel Grid-based Crowding Distance for Multimodal Multi-objective Optimization[C]//2020 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2020: 1-8.（paper）

  25. C. Rivera, M. Inostroza-Ponta, M. Villalobos-Cid. A multimodal multi-objective optimisation approach to deal with the phylogenetic inference problem[C]//2020 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB). IEEE, 2020: 1-7.（paper）

  26. Q. Lin, W. Lin, Z. Zhu, M. Gong, J. Li, C. A. Coello Coello. Multimodal Multi-objective Evolutionary Optimization with Dual Clustering in Decision and Objective Spaces[J]. IEEE Transactions on Evolutionary Computation, 2020, PP(99):1-1. (paper)(code)

  27. J. J. Liang, K. J. Qiao, C. T. Yue, K. J. Yu, Y. Hu. A Clustering-Based Differential Evolution Algorithm for Solving Multimodal Multi-Objective Optimization Problems[J]. Swarm and Evolutionary Computation, 2020.(paper)(code)

  28. B. Y. Qu, C. Li, J. Liang, L. Yan, K. J. Yu, Y. S. Zhu.  A self-organized speciation based multi-objective particle swarm optimizer for multimodal multi-objective problems[J]. Applied Soft Computing, 2020.(paper)(code)

  29. X. W. Zhang, H. Liu, L. P. Tu. A modified particle swarm optimization for multimodal multi-objective optimization[J]. Engineering Applications of Artificial Intelligence, 2020, 95: 103905.（paper）

  30. 岳彩通. 基于群集智能的多模态多目标优化算法及其应用研究[D]. 郑州: 郑州大学, 2020. (paper)

    C. T. Yue. Research  on  multimodal  multiobjective  optimization algorithm and application based on swarm intelligence [D]. Zhengzhou: Zhengzhou University, 2020. (paper)

  31. 李志梦. 用于多模态多目标优化的膝区间进化算法 [D]. 郑州: 郑州大学, 2020. (paper)

    Z. M. Li. Knee region evolution algorithm for multimodal multiobjective optimization [D]. Zhengzhou: Zhengzhou University, 2020. (paper)

  32. 位盼盼. 基于多模态多目标进化的集成学习器的选择及优化研究 [D]. 郑州: 郑州大学, 2020. (paper)

    P. P. Wei. Research on selection and optimization of ensemble learning based on multimodal multiobjective optimization [D]. Zhengzhou: Zhengzhou University, 2020. (paper)

  33. 李超. 自组织物种形成的多模态多目标粒子群算法的研究与应用 [D]. 郑州: 中原工学院, 2020. (paper)

    C. Li. The research and applicationof multimodal multiobjective particle swarm optimization for self-organizing speciation [D]. Zhengzhou: Zhongyuan University of Technology, 2020. (paper)

  34. 王铂. 基于多模态多目标差分进化的集成极限学习机算法研究 [D]. 郑州: 郑州大学, 2020. (paper)

    B. Wang. Research on ensemble extreme learning machine algorithm based on multimodal and multi-objective differential evolution [D]. Zhengzhou: Zhengzhou University, 2020. (paper)

  35. 胡晨旭. 多目标演化优化算法的决策空间多样性维护机制研究 [D]. 哈尔滨: 哈尔滨工业大学, 2020. (paper)

    C. X. Hu. Incorporation of a decision space diversity maintenance mechanism into evolutionary multi-objective optimization algorithms [D]. Harbin: Harbin Institute of Technology, 2020. (paper)

  36. 李国森,闫李,郭倩倩,周同驰,王永林,岳彩通. 基于参考点的多模态多目标粒子群算法 [J]. 计算机应用与软件, 2020,37 11 198-205. (paper)

    G. S. Li, L. Yan, Q. Q. Guo, T. C. Zhou, Y. L. Wang, C. T. Yue. Reference-point-based multimodal multi-objective particle swarm optimization [J]. Computer Applications and Software, 2020,37 11 198-205. (paper)

  37. 汪慎文,王佳莹,高娜,周瑶. 结合两种拓扑结构的多模态多目标粒子群优化算法 [J]. 南昌工程学院学报,2020,39(147), 04 70-75+99. (paper)

    S. W. Wang, J. Y. Wang, N. Gao, Y. Zhou. Multi-modal and multi-objective particle swarm optimization with two topology structure [J]. Journal of Nanchang Institute of Technology,2020,39(147), 04 70-75+99. (paper)

  38. 高海军,潘大志. 星型结构的多目标粒子群算法求解多模态多目标问题 [J]. 计算机工程与科学,2020,42(308), 08 145-154. (paper)

    H. J. Gao, D. Z. Pan. A multi-objective particle swarm optimization algorithm with star structure to solve the multi-modal multi-objective problem [J]. Computer Engineering and Science,2020,42(308), 08 145-154. (paper)

  39. 闫李,李国森,瞿博阳,朱小培,马佳慧. 基于双层协同进化的多目标粒子群算法 [J]. 计算机工程与设计,2020,41(407), 11 137-144. (paper)

    Y. Li, G. S. Li, B. Y. Qu, X. P. Zhu, J. H. Ma. Double-layer co-evolutionary multi-objective particle swarm optimization algorithm [J]. Computer Engineering and Design,2020,41(407), 11 137-144. (paper)

  40. Q. Q. Fan, X. F. Yan. Solving Multimodal Multiobjective Problems Through Zoning Search, IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019.(paper)

  41. W. Z. Zhang , G. S. Li , W. W. Zhang, J. J. Liang, G. Y. Gary. A cluster based PSO with leader updating mechanism and ring-topology for multimodal multi-objective optimization[J]. Swarm and Evolutionary Computation, 2019.(paper)

  42. R. Tanabe; and H. Ishibuchi, A Review of Evolutionary Multi-modal Multi-objective Optimization, IEEE Transactions on Evolutionary Computation, 2019.(paper)

  43. C. T. Yue, J. J. Liang, B. Y. Qu, K. J. Yu, H. Song, Multimodal Multiobjective Optimization in Feature Selection, IEEE Congress on Evolutionary Computation, 2019, pp. 302-309.(paper)

  44. L. Yan, G. S. Li, Y. C. Jiao, B. Y. Qu, C. T. Yue, S. K. Qu, A Performance Enhanced Niching Multi-objective Bat algorithm for Multimodal Multi-objective Problems, IEEE Congress on Evolutionary Computation, 2019, pp. 1275-1282.(paper)

  45. R. Z. Shi, W. Lin, Q. Z. Lin, Z. X. Zhu, J. Y. Chen, Multimodal Multi-Objective Optimization Using A Density-based One-by-One Update Strategy, IEEE Congress on Evolutionary Computation, 2019, pp. 295-301.(paper)

  46. K. Maity, R. Sengupta, S. Sha, MM-NAEMO : Multimodal Neighborhood-sensitive Archived Evolutionary Many-objective Optimization Algorithm, IEEE Congress on Evolutionary Computation, 2019, pp. 286-294.(paper)

  47. Y. Liu, H. Ishibuchi, Y. Nojima, N. Masuyama, Y. Han, Searching for Local Pareto Optimal Solutions: A Case Study on Polygon-Based Problems, IEEE Congress on Evolutionary Computation, 2019, pp. 896-903.(paper)

  48. S. Maree, T. Alderliesten, P. Bosman, Real-valued evolutionary multi-modal multi-objective optimization by hill-valley clustering, Genetic and Evolutionary Computation Conference, 2019, pp. 568-576.(paper)

  49. Z. H. Li , L. Shi, C. T. Yue, Z. G. Shang, B. Y. Qu. Differential evolution based on reinforcement learning with fitness ranking for solving multimodal multiobjective problems[J]. Swarm and Evolutionary Computation, 49: 234-244, 2019.（paper）

  50. C. T. Yue, B. Y. Qu, K. J. Yu, J. J. Liang, X. D. Li. A Novel Scalable Test Problem Suite for Multimodal Multiobjective Optimization, Swarm and Evolutionary Computation, vol. 48, pp. 62-71, 2019. （paper）(code)

  51. J. J. Liang, W. Xu, C. Yue, K. Yu, H. Song, O. D. Crisalle, and B. Qu, “Multimodal Multiobjective Optimization with Diffierential Evolution,” Swarm and Evolutionary Computation, vol. 44, pp. 1028-1059, 2018.（paper）(code)

  52. Y. Hu, J. Wang, J. Liang, K. Yu, H. Song, Q. Guo, C. Yue, Y. Wang. A self-organizing multimodal multi-objective pigeon-inspired optimization algorithm[J]. SCIENCE CHINA Information Sciences, 2019, 62(7): 1-17.（paper）（code）

  53. 许伟伟, 梁静, 岳彩通, 瞿博阳. 多模态多目标差分进化算法求解非线性方程组[J]. 计算机应用研究. 2019,36(331), 05 31-36.（paper）（code）

    W. W. Xu, J. J. Liang, C. T. Yue, B. Y. Qu. Multimodal multi-objective differential evolution algorithm for solving nonlinear equations [J]. Application Research of Computers, 2019,36(331), 05 31-36.（paper）（code）

  54. 李国庆. 面向复杂多模态多目标优化问题的粒子群算法研究 [D]. 郑州: 郑州轻工业大学, 2019. (paper)

    G. Q. Li. Research on particle swarm optimization algorithm multimodal multi-objective optimization problems [D]. Zhengzhou: Zhengzhou University of Light Industry, 2019. (paper)

  55. 李国森. 多模态多目标进化算法的研究与应用 [D]. 郑州: 中原工学院, 2019. (paper)

    G. S. Li. The research and application of multimodal multi-objective algorithms [D]. Zhengzhou: Zhongyuan University of Technology, 2019. (paper)

  56. 许伟伟. 多模态多目标差分进化算法研究及在非线性方程组的应用 [D]. 郑州: 郑州大学, 2018. (paper)

    W. W. Xu. Multimodal multi-objective differential evolution algorithm and its application in nonlinear equations [D]. Zhengzhou: Zhengzhou University, 2018. (paper)

  57. 郭倩倩. 基于自组织映射网络的多目标粒子群优化算法 [D]. 郑州: 郑州大学, 2018. (paper)

    Q. Q. Guo. A multi-objective particle swarm optimization algorithm based on self-organizing map network [D]. Zhengzhou: Zhengzhou University, 2018. (paper)

  58. J. Liang, Q. Q. Guo, C. T. Yue, B. Y. Qu, K. J. Yu. A self-organizing multi-objective particle swarm optimization algorithm for multimodal multi-objective problems[C]// International Conference on Swarm Intelligence. Springer, Cham, 2018: 550-560.（paper）(code)

  59. C. T. Yue, B. Y. Qu, J. J. Liang. A multiobjective particle swarm optimizer using ring topology for solving multimodal multiobjective problems[J]. IEEE Transactions on Evolutionary Computation, 2018, 22(5): 805-817.(paper)（code）

  60. Y. Liu, G. G. Yen and D. Gong. A multi-modal multi-objective evolutionary algorithm using two-archive and recombination strategies, IEEE Transactions on Evolutionary Computation, 2018, Early Access. DOI: 10.1109/TEVC.2018.2879406. (paper) (code)

  61. R. Tanabe, H. Ishibuchi. A decomposition-based evolutionary algorithm for multi-modal multi-objective optimization[C]// International Conference on Parallel Problem Solving from Nature. 2018, 261: 249-261.（paper）

  62. Y. Liu, H. Ishibuchi, Y. Nojima, N. Masuyama, K. Shang. A double-niched evolutionary algorithm and its behavior on polygon-based problems[C]// International Conference on Parallel Problem Solving from Nature. 2018, 261: 262-273.（paper）

  63. T. Tušar, D. Brockhoff, N. Hansen, A. Auger. COCO: The bi-objective black box optimization benchmarking (bbob-biobj) test suite[J], ArXiv e-prints, 2016.（paper）

  64. P. Kerschke, C. Grimme. An expedition to multimodal multi-objective optimization landscapes[C]// International Conference on Evolutionary Multi-Criterion Optimization, 2017: 329-343.（paper）

  65. J. J. Liang,  C. T. Yue,  B. Y. Qu. Multimodal multi-objective optimization: A preliminary study[C]// Evolutionary Computation. IEEE, 2016: 2454-2461.（paper）（code）

  66. P. Kerschke, H. Wang, M. Preuss, C. Grimme, A. Deutz, H. Trautmann, M. Emmerich. Towards analyzing multimodality of continuous multiobjective landscapes[C]// International Conference on Parallel Problem Solving from Nature, 2016: 962-972.（paper）

  67. H. Masuda,  Y. Nojima,  H. Ishibuchi. Visual examination of the behavior of EMO algorithms for many-objective optimization with many decision variables[C]// Evolutionary Computation. IEEE, 2014: 2633-2640.（paper）

  68. H. Ishibuchi, M. Yamane, N. Akedo, Y. Nojima. Many-objective and many-variable test problems for visual examination of multiobjective search[C]// Evolutionary Computation. IEEE, 2013: 1491-1498.（paper）

  69. O. Schütze, M. Vasile, C. A. Coello Coello. Computing the set of epsilon-efficient solutions in multiobjective space mission design[J]. Journal of Aerospace Computing, Information, and Communication, 2011, 8(3): 53-70. (paper)

  70. H. Ishibuchi,  N. Akedo, Y. Nojima. A many-objective test problem for visually examining diversity maintenance behavior in a decision space[C]// Conference on Genetic & Evolutionary Computation. ACM, 2011: 649-656.（paper）

  71. H. Ishibuchi, Y. Hitotsuyanagi, N. Tsukamoto, Y. Nojima. Many-objective test problems to visually examine the behavior of multiobjective evolution in a decision space[C]// International Conference on Parallel Problem Solving from Nature. Springer-Verlag, 2010: 91-100.（paper）

  72. O. Kramer, H. Danielsiek. Dbscan-based multi-objective niching to approximate equivalent pareto-subsets[C]//Proceedings of the 12th annual conference on Genetic and evolutionary computation. ACM, 2010: 503-510. (paper)

  73. A. Saha, K. Deb. A bi-criterion approach to multimodal optimization: Self-adaptive approach[C]//Asia-Pacific Conference on Simulated Evolution and Learning. Springer, Berlin, Heidelberg, 2010: 95-104. (paper)

  74. O. M. Shir, M. Preuss, B. Naujoks, M. Emmerich. Enhancing decision space diversity in evolutionary multiobjective algorithms[C]//International Conference on Evolutionary Multi-Criterion Optimization. Springer, Berlin, Heidelberg, 2009: 95-109. (paper)

  75. M. Preuss, G. Rudolph, F. Tumakaka. Solving multimodal problems via multiobjective techniques with Application to phase equilibrium detection[C]//2007 IEEE Congress on Evolutionary Computation. IEEE, 2007: 2703-2710. (paper)

  76. M. Preuss, B. Naujoks, G. Rudolph. Pareto set and emoa behavior for simple multimodal multiobjective functions[J]. Lecture Notes in Computer Science, 2006, 4193:513-522. (paper)

  77. K. Deb, S. Tiwari. Omni-optimizer: a procedure for single and multi-objective optimization[C]// Evolutionary Multi-criterion Optimization, Third International Conference, Emo, Guanajuato, Mexico, March. DBLP, 2005: 47-61.（paper）

  78. R. Kumar, P. Rockett. Effective evolutionary multimodal optimization by multiobjective reformulation without explicit niching/sharing[C]//Asian Applied Computing Conference. Springer, Berlin, Heidelberg, 2004: 1-8. (paper)

  79. K. Deb. Multi-objective genetic algorithms: problem difficulties and construction of test problems[J]. Evolutionary Computation, 1999, 7(3):205-230.（paper）



 



附件【Multimodal Multi-objective Optimization A Preliminary Study.rar】
附件【A novel scalable test problem suite for multimodal multiobjective optimization (with appendix).pdf】

Links

Computional Intelligence of Zhengzhou University